Bilgisayar Özelliklerinin İncelenmesi ve Matris Çarpma İşlemine Etkisi.
Karadeniz Teknik Üniversitesi
Bilgisayar Mühendisliği Bölümü
Paralel Bilgisayarlar
Ad&Soyad: Nurullah Demirci
Sistem Bilgileri
~? Bilgisayarımızın FLOP/s kapasitesi nedir. ?~
FLOP/s Nedir? -> Saniyedeki kayan noktalı sayı ile yapılan (floating-point number) işlem sayısıdır. Mikroişlemcilerin hız performansını göstermek için kullanılan bir ölçüdür. Özellikle aşırı derecede kayan noktalı sayı işlemleri içeren bilimsel işlemlerde bu ölçüt kullanılır. Kayan noktalı işlemler kesirli sayılarla yapılan işlemleri içerir ve bu işlemler tam sayılar ile yapılan işlemlerden daha uzun sürer ve daha zordur. Çoğu modern işlemci kayan noktalı sayı işlemlerini yapmak için özel FPU (Floating Point Unit) birimini içerir.
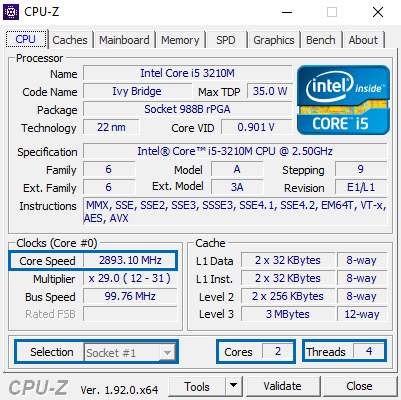
Bilgisayarımızın İşlemcisi İntel(R) Core i5 3210M 2.5Ghz - 3.1Ghz
FLOP/s HESABI: Soket Sayısı * Soket Başına Çekirdek Sayısı * Saniye Başına Saat Döngü Sayısı * Döngü Başına Kayan Nokta İşlemi Sayısı
FLOP/s => 1 * 2 * 3.1Ghz * 4 = 24.8 GFLOPS
Bilgisayarımızın Grafik Kartı NVIDIA GeForce GT 635M
FP32 (float) performance: 388.8 GFLOPS
FP64 (double) performance: 32.40 GFLOPS
Bilgisayarımızın 2. Grafik Kartı Intel(R) HD Graphics 4000
FP32 (float) performance: 256.0 GFLOPS
FP64 (double) performance: 64.0 GFLOPS
~? Sistemindeki Cache belleğin özelliklerini açıklayınız, I-Cache, D-Cache kapasiteleri nedir. ?~
Cache Bellek (Önbellek)? -> CPU çok hızlıdır ve sürekli olarak hafızadan veri okur. Sistem belleğinden gelen veriler ise çoğunlukla CPU’nun hızına yetişemez ve işlemci verinin ulaşmasını beklemek zorunda kalır. Bu problemi çözmek için CPU içinde yüksek hızlı hafızalar bulunur, buna önbellek(cache) denir. Ön bellek çalışmakta olan programa ait komutların, verilerin geçici olarak saklandığı yüksek hızlı hafızalardır.
♦ L1 ön bellek (cache) : Önemli kodlar ve veriler bellekten buraya kopyalanır ve işlemci bunlara daha hızlı ulaşabilir. Kodlar için olan Code cache ve veriler için olan Data cache olmak üzere ikiye ayrılır. Kapasitesi 2 KB ile 256 KB arasında değişir.
L1 I-Cache: Instruction Cache, yani işlemcinin desteklediği komut setlerinin saklandığı ön bellektir.
L1 D-Cache: Data Cache, yani verilerin saklandığı ön bellek.
♦ L2 ön bellek (cache) : L1 belleklerine göre kapasiteleri 256 KB ile 2 MB arasında değişir. Başlangıçta L2 önbellek anakart üzerinde işlemciye yakın bir yerde yer almaktaydı. Daha sonra slot işlemciler ortaya çıkınca işlemci çekirdeğinin üzerinde kartuş şeklindeki paketlerde yer aldı. Bununla beraber çekirdeğin dışında ve işlemciyle aynı yapıda kullanılmaya başlandı. Bu kısa geçiş döneminden sonraysa L2 önbellek işlemci çekirdeklerine entegre edildi.
♦ L3 ön bellek (cache): L3 ön belleklerinin kapasiteleri 2MB ile 256 MB arasında değişir. Yeni bir teknolojidir. Çok çekirdekli işlemcilerde bütün çekirdeklere tek bir bellekle hizmet vermek akıllıca bir yaklaşım olacağı düşüncesiyle geliştirilmiştir.
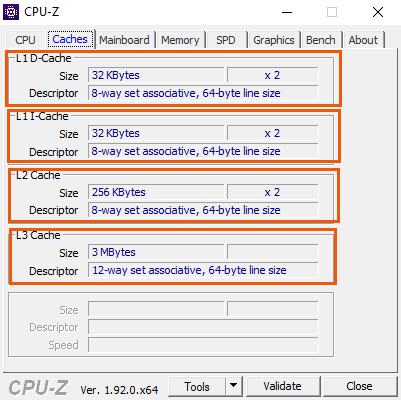
Bilgisayarımın I-Cache Kapasitesi: 32 KByte x 2
Bilgisayarımın D-Cache Kapasitesi: 32 KByte x 2
~? Tampon bellekler için 4-yönlü (4-way) ne demektir. ?~
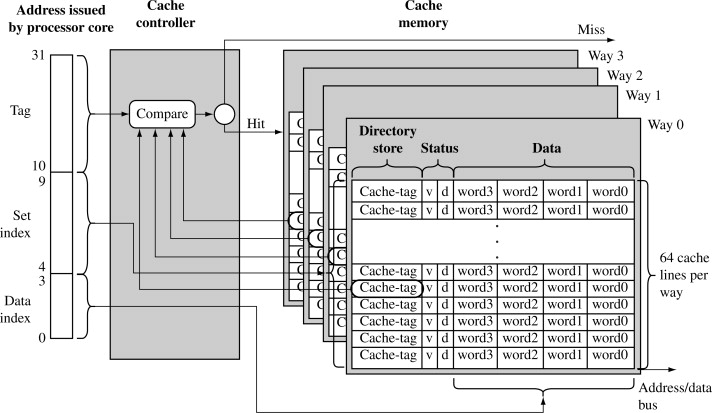
Cache’de, Ana hafızada bulunan adres bloklarından daha az 'line' olduğu için bir haritalama fonksiyonuna ihtiyaç vardır.
Kullanılabilecek 3 teknik var:
Doğrudan
Asosyatif
Küme Asosyatif

4-yönlü(4-way) küme asosyatif'e dahildir. Cache belirli bir sayıda küme içerir. Her küme belirli bir sayıda line içerir. Bir ana hafıza bloğu, belirli bir küme içerisindeki herhangi bir line ile eşleştirilebilir.
Ör: Bir kümede 4 line olsun. 4-way asosyatif Bir ana hafıza bloğu, belirli olan bir küme içerisindeki 4 line’dan biri ile eşleşir.
Kodlama Bölümü
~~ Projede nxn boyutlu 2 matrisin çarpımı yapılmıştır. Ayrıca proje hem seri hem de paralel kodlanmıştır. Kodlar aşağıdaki gibidir. ~~
#define WHITE SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_RED | FOREGROUND_GREEN | FOREGROUND_BLUE);
#define RED SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_RED);
#define GREEN SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_GREEN);
#define BLUE SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_BLUE);
#define YELLOW SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_RED | FOREGROUND_GREEN);
#define MAGENTA SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_RED | FOREGROUND_BLUE);
#define CYAN SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_GREEN | FOREGROUND_BLUE);
#define GRAY SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY);
#define HAVE_STRUCT_TIMESPEC
#include <pthread.h>
#include <windows.h>
#include <iostream>
#include <iomanip>
#include <ctime>
#define SIZE 1000 // 1K 2K 3K 4K 5K
#define PRINT_SIZE 10 // JUST PRINT_SIZE ELEMENT WILL PRINT OUTPUT SCREEN
#define THREAD 10 // THREAD COUNT
//using namespace std;
pthread_t threads[THREAD]; // CREATE THREADS
pthread_mutex_t mutex; // = PTHREAD_MUTEX_INITIALIZER;
pthread_cond_t cond; // = PTHREAD_COND_INITIALIZER;
int core;
template <typename T> T** A;
template <typename T> T** B;
template <typename T> T** S;
// STRCUT FOR MATRIX(2D ARRAY)
template <class Type>
struct TypeMatrix {
Type** Mtrx;
};
// Matrix CLASS SPECIFIED
template <class Type>
class Matrix {
private:
Type _X, _Y;
struct TypeMatrix<Type> X; // nxn <TYPE> MATRIX X (n = SIZE)
struct TypeMatrix<Type> Y; // nxn <TYPE> MATRIX Y (n = SIZE)
struct TypeMatrix<Type> R; // nxn <TYPE> MATRIX RESULT (n = SIZE)
public:
Matrix(Type _x = (Type)1., Type _y = (Type)2.); // CONSTRUCTOR
void Create_Matrix(); // MATRIX CREATE METHOD
void Multiply_Matrix(); // MATRIX ELEMENTWISE MULTIPLICATION METHOD
void Multiply_Matrix_With_Threads(std::string); // THREADS CREATE AND JOIN METHOD
static void *Block_Mutiply_Matrix(void *); // BLOCK THREAD METHOD
static void *Squential_Mutiply_Matrix(void *); // SQUENTIAL THREAD METHOD
void Print(); // MATRIX PRINT METHOD
~Matrix();
};
// CONSTRUCTOR <TYPE> MATRIX CREATING (X && Y && R)
template <class Type>
Matrix<Type>::Matrix(Type _x, Type _y) {
this->_X = _x;
this->_Y = _y;
Create_Matrix();
}
// <TYPE> MATRIX CREATE METHOD (X && Y && R)
template <class Type>
void Matrix<Type>::Create_Matrix() {
X.Mtrx = new Type*[SIZE];
Y.Mtrx = new Type*[SIZE];
R.Mtrx = new Type*[SIZE];
for (int i = 0; i < SIZE; i++) {
X.Mtrx[i] = new Type[SIZE];
Y.Mtrx[i] = new Type[SIZE];
R.Mtrx[i] = new Type[SIZE];
for (int j = 0; j < SIZE; j++) {
X.Mtrx[i][j] = (Type)_X;
Y.Mtrx[i][j] = (Type)_Y;
R.Mtrx[i][j] = (Type)0.;
}
}
}
// <TYPE> MATRIX ELEMENTWISE MULTIPLICATION METHOD
template <class Type>
void Matrix<Type>::Multiply_Matrix() {
Type Total = (Type)0.;
for (int i = 0; i < SIZE; i++) {
for (int j = 0; j < SIZE; j++) {
for (int k = 0; k < SIZE; k++) {
Total += X.Mtrx[i][k] * Y.Mtrx[k][j];
}
R.Mtrx[i][j] = Total;
Total = (Type)0.;
}
}
}
// THREADS CREATE AND JOIN METHOD
template <class Type>
void Matrix<Type>::Multiply_Matrix_With_Threads(std::string DataShareType){
A<Type> = new Type*[SIZE];
B<Type> = new Type*[SIZE];
S<Type> = new Type*[SIZE];
for (int i = 0; i < SIZE; i++){
A<Type>[i] = new Type[SIZE];
B<Type>[i] = new Type[SIZE];
S<Type>[i] = new Type[SIZE];
for (int j = 0; j < SIZE; j++){
A<Type>[i][j] = X.Mtrx[i][j];
B<Type>[i][j] = Y.Mtrx[i][j];
S<Type>[i][j] = R.Mtrx[i][j];
}
}
core = 0;
pthread_mutex_init(&mutex, NULL);
pthread_cond_init(&cond, NULL);
for (int i = 0; i < THREAD; i++){
if (DataShareType == "BlockDataShare")
pthread_create(&threads[i], NULL, Block_Mutiply_Matrix, NULL);
else if (DataShareType == "SquentialDataShare")
pthread_create(&threads[i], NULL, Squential_Mutiply_Matrix, NULL);
else
std::cout << " UNDEFINE DATA SHARE TYPE \n";
}
for (int i = 0; i < THREAD; i++)
pthread_join(threads[i], NULL);
pthread_mutex_destroy(&mutex);
pthread_cond_destroy(&cond);
for (int i = 0; i < SIZE; i++) {
for (int j = 0; j < SIZE; j++) {
R.Mtrx[i][j] = S<Type>[i][j];
}
}
for (int i = 0; i < SIZE; i++) {
delete A<Type>[i];
delete B<Type>[i];
delete S<Type>[i];
}
delete[] A<Type>;
delete[] B<Type>;
delete[] S<Type>;
//std::cout << "~~~ A && B && S MATRIX DELETED ~~~\n";
}
// BLOCK DATA SHARE <TYPE> MATRIX ELEMENTTWISE MULTIPLICATION MATRIX WITH PTHREAD
template <class Type>
void *Matrix<Type>::Block_Mutiply_Matrix(void *) {
Type Total = (Type)0.;
int _core = core++;
for (int i = _core * SIZE / THREAD; i < (_core + 1) * SIZE / THREAD; i++) {
for (int j = 0; j < SIZE; j++) {
for (int k = 0; k < SIZE; k++) {
Total += A<Type>[i][k] * B<Type>[k][j];
}
S<Type>[i][j] = Total;
Total = (Type)0.;
}
}
pthread_exit(NULL);
return 0;
}
// SQUENTIAL DATA SHARE <TYPE> MATRIX ELEMENTTWISE MULTIPLICATION MATRIX WITH PTHREAD
template <class Type>
void *Matrix<Type>::Squential_Mutiply_Matrix(void *) {
Type Total = (Type)0.;
int _core = core++;
for (int i = 0; i < SIZE; i++) {
for (int j = 0; j < SIZE; j++) {
for (int k = _core * SIZE / THREAD; k < (_core + 1) * SIZE / THREAD; k++) {
Total += A<Type>[i][k] * B<Type>[k][j];
}
pthread_mutex_lock(&mutex);
S<Type>[i][j] += Total;
pthread_mutex_unlock(&mutex);
Total = (Type)0.;
}
}
pthread_exit(NULL);
return 0;
}
// <TYPE> MATRIX PRINT METHOD (DEBUG OUTPUT SCREEN)
template <class Type>
void Matrix<Type>::Print() {
for (int i = 0; i < PRINT_SIZE; i++) {
std::cout << "[";
for (int j = 0; j < PRINT_SIZE; j++) {
if (j != PRINT_SIZE - 1)
std::cout << std::fixed << std::setprecision(2) << R.Mtrx[i][j] << ", ";
else
std::cout << std::fixed << std::setprecision(2) << R.Mtrx[i][j];
}
std::cout << "]\n";
}
}
// DESTRUCTOR
template <class Type>
Matrix<Type>::~Matrix(){
for (int i = 0; i < SIZE; i++) {
delete X.Mtrx[i];
delete Y.Mtrx[i];
delete R.Mtrx[i];
}
delete[] X.Mtrx;
delete[] Y.Mtrx;
delete[] R.Mtrx;
//std::cout << "~~~ X && Y && R MATRIX DELETED ~~~\n";
}
// MAIN METHOD
int main() {
double time; // TIME VARIABLE
CYAN; std::cout << "\n~~ " << SIZE << "*" << SIZE << " Iki Matris Carpimi Sonuclari ~~\n\n"; WHITE;
// DOUBLE MATRIX ELEMENTWISE MULTIPLICATION OPERATIONS (SERIAL EXCUTE)
Matrix<double> D__EMUL; // OBJECT SPECIFIED
clock_t start__1 = clock(), finish__1; // EXCUTE TIME START
D__EMUL.Multiply_Matrix(); // EXCUTE METHOD
finish__1 = clock(); // EXCUTE TIME FINISH
//D__EMUL.Print(); // DEBUG OUTPUT SCREEN
time = (double)(finish__1 - start__1) / CLOCKS_PER_SEC; // TIME CALCULATION
GREEN;
std::cout << "~~~ DOUBLE MULTIPLICATION MATRIX EXCUTE TIME (SERIAL): " << time << " ~~~\n\n";
WHITE;
// FLOAT MATRIX ELEMENTWISE MULTIPLICATION OPERATIONS (SERIAL EXCUTE)
Matrix<float> F__EMUL; // OBJECT SPECIFIED
clock_t start__11 = clock(), finish__11; // EXCUTE TIME START
F__EMUL.Multiply_Matrix(); // EXCUTE METHOD
finish__11 = clock(); // EXCUTE TIME FINISH
//F__EMUL.Print(); // DEBUG OUTPUT SCREEN
time = (double)(finish__11 - start__11) / CLOCKS_PER_SEC; // TIME CALCULATION
YELLOW;
std::cout << "~~~ FLOAT MULTIPLICATION MATRIX EXCUTE TIME (SERIAL): " << time << " ~~~\n\n";
WHITE;
// BLOCK DATA DOUBLE MATRIX ELEMENTWISE MULTIPLICATION OPERATIONS (PARALLELISM EXCUTE WITH pThread)
Matrix<double> DB__EMUL; // OBJECT SPECIFIED
clock_t start__2 = clock(), finish__2; // EXCUTE TIME START
DB__EMUL.Multiply_Matrix_With_Threads("BlockDataShare"); // MUST BE DEFINE ( "BlockDataShare" || "SquentialDataShare" )
finish__2 = clock(); // EXCUTE TIME FINISH
//DB__EMUL.Print(); // DEBUG OUTPUT SCREEN
time = (double)(finish__2 - start__2) / CLOCKS_PER_SEC; // TIME CALCULATION
GREEN;
std::cout << "~~~ BLOCK DATA DOUBLE MULTIPLICATION MATRIX WITH THREADS EXCUTE TIME (PARALLEL): " << time << " ~~~\n\n";
WHITE;
// SQUENTIAL DATA DOUBLE MATRIX ELEMENTWISE MULTIPLICATION OPERATIONS (PARALLELISM EXCUTE WITH pThread)
Matrix<double> DS__EMUL; // OBJECT SPECIFIED
clock_t start__3 = clock(), finish__3; // EXCUTE TIME START
DS__EMUL.Multiply_Matrix_With_Threads("SquentialDataShare");// MUST BE DEFINE ( "BlockDataShare" || "SquentialDataShare" )
finish__3 = clock(); // EXCUTE TIME FINISH
//DS__EMUL.Print(); // DEBUG OUTPUT SCREEN
time = (double)(finish__3 - start__3) / CLOCKS_PER_SEC; // TIME CALCULATION
YELLOW;
std::cout << "~~~ SQUENTIAL DATA DOUBLE MULTIPLICATION MATRIX WITH THREADS EXCUTE TIME (PARALLEL): " << time << " ~~~\n\n";
WHITE;
// BLOCK DATA FLOAT MATRIX ELEMENTWISE MULTIPLICATION OPERATIONS (PARALLELISM EXCUTE WITH pThread)
Matrix<float> FB__EMUL; // OBJECT SPECIFIED
clock_t start__22 = clock(), finish__22; // EXCUTE TIME START
FB__EMUL.Multiply_Matrix_With_Threads("BlockDataShare"); // MUST BE DEFINE ( "BlockDataShare" || "SquentialDataShare" )
finish__22 = clock(); // EXCUTE TIME FINISH
//FB__EMUL.Print(); // DEBUG OUTPUT SCREEN
time = (double)(finish__22 - start__22) / CLOCKS_PER_SEC; // TIME CALCULATION
GREEN;
std::cout << "~~~ BLOCK DATA FLOAT MULTIPLICATION MATRIX WITH THREADS EXCUTE TIME (PARALLEL): " << time << " ~~~\n\n";
WHITE;
// SQUENTIAL DATA FLOAT MATRIX ELEMENTWISE MULTIPLICATION OPERATIONS (PARALLELISM EXCUTE WITH pThread)
Matrix<float> FS__EMUL; // OBJECT SPECIFIED
clock_t start__33 = clock(), finish__33; // EXCUTE TIME START
FS__EMUL.Multiply_Matrix_With_Threads("SquentialDataShare");// MUST BE DEFINE ( "BlockDataShare" || "SquentialDataShare" )
finish__33 = clock(); // EXCUTE TIME FINISH
//FS__EMUL.Print(); // DEBUG OUTPUT SCREEN
time = (double)(finish__33 - start__33) / CLOCKS_PER_SEC; // TIME CALCULATION
YELLOW;
std::cout << "~~~ SQUENTIAL DATA FLOAT MULTIPLICATION MATRIX WITH THREADS EXCUTE TIME (PARALLEL): " << time << " ~~~\n\n";
WHITE;
return 0;
}
~~ Kodların Görsel Olarak Görünümü ve Bazı Testlerin Sonuçları Aşağıdaki Gibidir. ~~
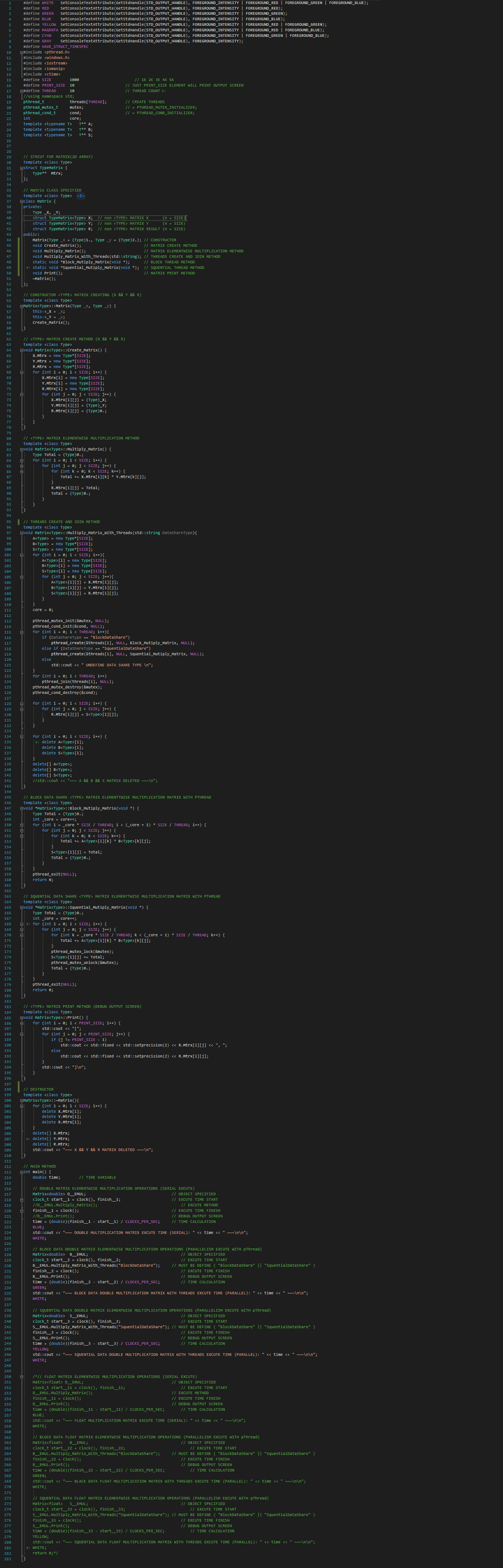
Projede nxn boyutlu 2 matrisin çarpımını yapılmaktadır. Proje hem seri hem de paralel kodlanmıştır. Matrisler '1.0' ve '2.0' değerleri ile doldurulmuştur. Matrisler dinamik tanımlanmıştır. Bu sayede n = 1K, 2K, 3K, 4K, 5K (K: Bin) sadece n değeri değiştirilerek oluşturulabilir. Kodlamada C++ ve pThread Kullanılmıştır. Hem Float, hem de Double matrix çarpımları için C++ template özelliği kullanılmıştır.
~~ Kodumuzu Seri ve 10 Thread ile Test Edip Sonuçlarını Görelim ~~
1K x 1K Matris Çarpımı:
Double Değer Tanımlı Matrisler Seri Çalışma Süresi: 15.088sn Float Değer Tanımlı Matrisler Seri Çalışma Süresi: 11.09sn Double Değer Tanımlı Matrisler Blok Veri Paylaşımı Paralel Çalışma Süresi: 5.688sn Double Değer Tanımlı Matrisler Ardışıl Veri Paylaşımı Paralel Çalışma Süresi: 4.868sn Float Değer Tanımlı Matrisler Blok Veri Paylaşımı Paralel Çalışma Süresi: 4.813sn Float Değer Tanımlı Matrisler Ardışıl Veri Paylaşımı Paralel Çalışma Süresi: 4.105sn
2K x 2K Matris Çarpımı:
Double Değer Tanımlı Matrisler Seri Çalışma Süresi: 164.172sn Float Değer Tanımlı Matrisler Seri Çalışma Süresi: 123.37sn Double Değer Tanımlı Matrisler Blok Veri Paylaşımı Paralel Çalışma Süresi: 67.969sn Double Değer Tanımlı Matrisler Ardışıl Veri Paylaşımı Paralel Çalışma Süresi: 38.381sn Float Değer Tanımlı Matrisler Blok Veri Paylaşımı Paralel Çalışma Süresi: 48.979sn Float Değer Tanımlı Matrisler Ardışıl Veri Paylaşımı Paralel Çalışma Süresi: 29.042sn
3K x 3K Matris Çarpımı:
Double Değer Tanımlı Matrisler Seri Çalışma Süresi: 450.104sn Float Değer Tanımlı Matrisler Seri Çalışma Süresi: 379.546sn Double Değer Tanımlı Matrisler Blok Veri Paylaşımı Paralel Çalışma Süresi: 205.727sn Double Değer Tanımlı Matrisler Ardışıl Veri Paylaşımı Paralel Çalışma Süresi: 134.64sn Float Değer Tanımlı Matrisler Blok Veri Paylaşımı Paralel Çalışma Süresi: 226.329sn Float Değer Tanımlı Matrisler Ardışıl Veri Paylaşımı Paralel Çalışma Süresi: 121.95sn
4K x 4K Matris Çarpımı:
Double Değer Tanımlı Matrisler Seri Çalışma Süresi: 1130.25sn Float Değer Tanımlı Matrisler Seri Çalışma Süresi: 967.517sn Double Değer Tanımlı Matrisler Blok Veri Paylaşımı Paralel Çalışma Süresi: 537.798sn Double Değer Tanımlı Matrisler Ardışıl Veri Paylaşımı Paralel Çalışma Süresi: 367.762sn Float Değer Tanımlı Matrisler Blok Veri Paylaşımı Paralel Çalışma Süresi: 563.506sn Float Değer Tanımlı Matrisler Ardışıl Veri Paylaşımı Paralel Çalışma Süresi: 358.041sn
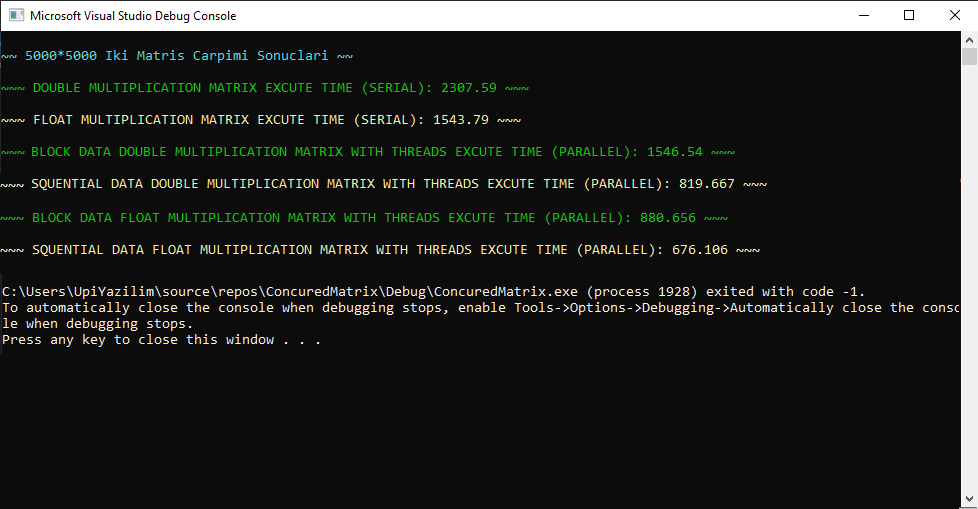
5K x 5K Matris Çarpımı:
Double Değer Tanımlı Matrisler Seri Çalışma Süresi: 2307.59sn Float Değer Tanımlı Matrisler Seri Çalışma Süresi: 1543.79sn Double Değer Tanımlı Matrisler Blok Veri Paylaşımı Paralel Çalışma Süresi: 1546.54sn Double Değer Tanımlı Matrisler Ardışıl Veri Paylaşımı Paralel Çalışma Süresi: 819.667sn Float Değer Tanımlı Matrisler Blok Veri Paylaşımı Paralel Çalışma Süresi: 880.656sn Float Değer Tanımlı Matrisler Ardışıl Veri Paylaşımı Paralel Çalışma Süresi: 676.106sn
~~ Kodların Görsel Olarak Görünümü ve Bazı Testlerin Sonuçları Aşağıdaki Gibidir. ~~
1K x 1K Matris Çarpımı Hızlanma && Verimlilik:
(Double Seri - Blok Veri Paylaşımı) Hızlanma = 15.088 / 5.688 = 2.65 (Double Seri - Blok Veri Paylaşımı) Verimlilik = (2.65 x 100) / 10 = 26.5% (Double Seri - Ardışıl Veri Paylaşımı) Hızlanma = 15.088 / 4.868 = 3.09 (Double Seri - Ardışıl Veri Paylaşımı) Verimlilik = (3.09 x 100) / 10 = 30.9% (Float Seri - Blok Veri Paylaşımı) Hızlanma = 11.09 / 4.813 = 2.30 (Float Seri - Blok Veri Paylaşımı) Verimlilik = (2.30 x 100) / 10 = 23% (Float Seri - Ardışıl Veri Paylaşımı) Hızlanma = 11.09 / 4.105 = 2.70 (Float Seri - Ardışıl Veri Paylaşımı) Verimlilik = (2.70 x 100) / 10 = 27%
2K x 2K Matris Çarpımı Hızlanma && Verimlilik:
(Double Seri - Blok Veri Paylaşımı) Hızlanma = 164.172 / 67.969 = 2.41 (Double Seri - Blok Veri Paylaşımı) Verimlilik = (2.41 x 100) / 10 = 24.1% (Double Seri - Ardışıl Veri Paylaşımı) Hızlanma = 164.172 / 38.381 = 4.27 (Double Seri - Ardışıl Veri Paylaşımı) Verimlilik = (4.27 x 100) / 10 = 42.7% (Float Seri - Blok Veri Paylaşımı) Hızlanma = 123.37 / 48.979 = 2.51 (Float Seri - Blok Veri Paylaşımı) Verimlilik = (2.51 x 100) / 10 = 25.1% (Float Seri - Ardışıl Veri Paylaşımı) Hızlanma = 123.37 / 29.042 = 4.24 (Float Seri - Ardışıl Veri Paylaşımı) Verimlilik = (4.24 x 100) / 10 = 42.4%
3K x 3K Matris Çarpımı Hızlanma && Verimlilik:
(Double Seri - Blok Veri Paylaşımı) Hızlanma = 450.104 / 205.727 = 2.18 (Double Seri - Blok Veri Paylaşımı) Verimlilik = (2.18 x 100) / 10 = 21.8% (Double Seri - Ardışıl Veri Paylaşımı) Hızlanma = 450.104 / 134.64 = 3.34 (Double Seri - Ardışıl Veri Paylaşımı) Verimlilik = (3.34 x 100) / 10 = 33.4% (Float Seri - Blok Veri Paylaşımı) Hızlanma = 379.546 / 226.329 = 1.67 (Float Seri - Blok Veri Paylaşımı) Verimlilik = (1.67 x 100) / 10 = 16.7% (Float Seri - Ardışıl Veri Paylaşımı) Hızlanma = 379.546 / 121.95 = 3.11 (Float Seri - Ardışıl Veri Paylaşımı) Verimlilik = (3.11 x 100) / 10 = 31.1%
4K x 4K Matris Çarpımı Hızlanma && Verimlilik:
(Double Seri - Blok Veri Paylaşımı) Hızlanma = 1130.25 / 537.798 = 2.10 (Double Seri - Blok Veri Paylaşımı) Verimlilik = (2.10 x 100) / 10 = 21.0% (Double Seri - Ardışıl Veri Paylaşımı) Hızlanma = 1130.25 / 367.762 = 3.07 (Double Seri - Ardışıl Veri Paylaşımı) Verimlilik = (3.07 x 100) / 10 = 30.7% (Float Seri - Blok Veri Paylaşımı) Hızlanma = 967.517 / 563.506 = 1.71 (Float Seri - Blok Veri Paylaşımı) Verimlilik = (1.71 x 100) / 10 = 17.1% (Float Seri - Ardışıl Veri Paylaşımı) Hızlanma = 967.517 / 358.041 = 2.70 (Float Seri - Ardışıl Veri Paylaşımı) Verimlilik = (2.70 x 100) / 10 = 27.0%
5K x 5K Matris Çarpımı Hızlanma && Verimlilik:
(Double Seri - Blok Veri Paylaşımı) Hızlanma = 2307.59 / 1546.54 = 1.49 (Double Seri - Blok Veri Paylaşımı) Verimlilik = (1.49 x 100) / 10 = 14.9% (Double Seri - Ardışıl Veri Paylaşımı) Hızlanma = 2307.59 / 819.667 = 2.81 (Double Seri - Ardışıl Veri Paylaşımı) Verimlilik = (2.81 x 100) / 10 = 28.1% (Float Seri - Blok Veri Paylaşımı) Hızlanma = 1543.79 / 880.656 = 1.75 (Float Seri - Blok Veri Paylaşımı) Verimlilik = (1.75 x 100) / 10 = 17.5% (Float Seri - Ardışıl Veri Paylaşımı) Hızlanma = 1543.79 / 676.106 = 2.28 (Float Seri - Ardışıl Veri Paylaşımı) Verimlilik = (2.28 x 100) / 10 = 22.8%
~? Sistemimizdeki Float ve Double Sürümlerinde Farklılık Var mıdır? Neden: ?~
Yukarıda da belirtildiği gibi test sonuçlarına bakıldığında Float veri tipi tanımlı matris çarpımları daha hızlı çalışmıştır. Double veri tipi tanımlı matris çarpımımız daha yavaş kaldı. Çünkü Float tipi kayan nokta sayısı, Double tipine göre daha azdır. Böylece işlemcilerin veya oluşturulan threadlerin yükleri daha az olur. Float hızlı sonuç vermiş olur.
~? Sistemimizde Belirtilen Flop/s Performans Limitinin Yüzde Kaçına Ulaşılabildi. ?~
Sistemimizi çalıştırdığımızda CPU çalışma hızımız 2.89Ghz kadar çıkıyor. Yani 1 * 2 * 2.89 * 4 = 23.12GFLOPS 93% performans limitine ulaşabildik.
~? Veri paylaşım türlerine göre uygulamamız geliştirilmiştir. Performans değişimleri vardır. Nedeni: ?~
Yukarıda da belirtildiği gibi test sonuçlarına bakıldığında Ardışıl veri paylaşım türü matris çarpım işlemi, Blok veri paylaşım türü matris çarpım işlemine göre daha hızlı çalışmıştır. Ardışıl veri paylaşım işleminde veri dağılım dengesi ve yük dağılımı daha iyi yapılıyor. Böylece threadler birbirini daha az bekliyor. Bunun sonucunda da daha hızlı sonuç veriyor.
~~ Matrix Çarpım İşlemlerinin Yorumu: ~~
Sistemin seri çalışması ile paralel çalışması 2 ile 4 arasında hızlanma ve 20% ile 40% arasında verimlilik sağlanmıştır. Küçük boyutlu matris çarpımlarında gereksiz görülebilir fakat eğer boyutumuz büyük verilerse zamandan tasarruf açısından çok önemli bir hızlanma değeri ortaya çıkmıştır.
